Blog

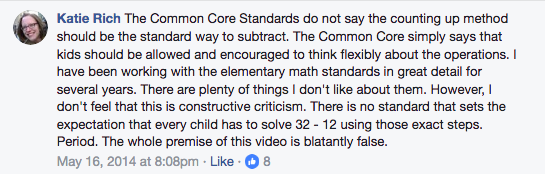
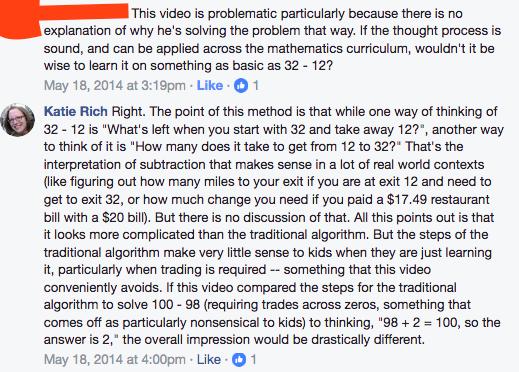
This week, I’m still thinking about curriculum materials and how they could be made more flexible and useful. I had two disparate experiences this week that ended up tying together to advance my thinking a bit from last week.

First, I read a study that traced the effects of a highly scripted curriculum resource on a preschool teacher’s instructional practices (Parks & Bridges-Rhoads, 2012). Despite the resource in question being a literacy curriculum, the highly scripted nature of the teacher’s interactions with students trickled into her math instruction. The article details the ways in which the scripting led to some missed opportunities to explore students’ mathematical thinking.

None of this was surprising to me, really. I had become convinced before that scripted curriculum can reduce a teacher’s opportunities for responsive teaching. (I want to emphasize the opportunities part here — neither the authors of the article nor I saw this research result as reflecting poorly on the teacher. If anything, it reflected poorly on the curriculum materials.) The problems with scripted curriculum don’t just live in early childhood, either. Developers of curriculum materials for students in middle school have recommended a shift from scripting to steering (Hoyles, Noss, Vahey, & Roschelle, 2013), especially in materials that are digitally based.

Dr. Amy Parks, the lead author of the preschool article, is now a faculty member at MSU. I had a chance to talk to her about this article, and we brainstormed some metaphors for navigating through a lesson that might be more conducive to responsive teaching than reading a script. One metaphor she had heard recently from a colleague was wayfinding, a kind of navigation that doesn’t involve use of a map, but rather reference to visible markers as you go. (It’s a cultural practice of Polynesians that recently got some attention via Disney’s Moana.) I really latched onto this. It made sense to me to think of the process of teaching as knowing where you want to go, and trusting that there will be markers along the way that give clues about how to get there.

This brought me back to the importance, and difficulty, of the number of in-the-moment decisions required in teaching. But it didn’t really get me any farther in thinking about how curriculum materials could be re-envisioned to better support teachers in their wayfinding. I understand that teachers don’t have the luxury of stopping to consult materials each time the classroom conversation takes an unexpected turn. Still, if we know that scripted materials are associated with less flexible teaching (Parks & Bridges-Rhoads, 2012), doesn’t it seem that there must be a different format for curriculum materials that could associate with wayfinding in teaching?

Enter my second relevant experience this week: delving into the history of research on educational technology. In his defense of research studying the effects of media on learning, Kozma (1991) highlighted research on nonlinear, hyperlinked text as an example of a then-emerging field of research of multimedia. He points to other research suggesting that use of hypertext supports cognitive flexibility, as navigation through the text supports making connections among concepts and themes: “[H]ypertext facilitates this cognitive flexibility because it allows a topic to be explored in multiple ways using a number of different concepts or themes” (Kozma, 1991, p. 202).

Exploring a topic in multiple ways feels similar to navigating through a lesson in multiple ways, don’t you think? Perhaps creating hyperlinked versions of curriculum materials, wherein teachers make decisions about what to read and in what order, is a way to move away from scripting and toward wayfinding.

There is a lot of exploration to be done on what links would be productive and useful for teachers, as well as how to deconstruct a curriculum into parts that can effectively be linked. Still, I think the idea could be a powerful one for giving teachers agency over curriculum decisions while still providing useful information via curriculum materials. I’m looking forward to delving into more hypermedia research to discover if anyone’s applied it to curriculum.

References

Hoyles, C., Noss, R., Vahey, P., & Roschelle, J. (2013). Cornerstone Mathematics: Designing digital technology for teacher adaptation and scaling. ZDM – International Journal on Mathematics Education, 45(7), 1057–1070.

Kozma, R. B. (1991). Learning with Media. Review of Educational Research, 61(2), 179–211.

Parks, A. N., & Bridges-Rhoads, S. (2012). Overly scripted: Exploring the impact of a scripted literacy curriculum on a preschool teacher’s instructional practices in mathematics. Journal of Research in Childhood Education, 26(3), 308–324.

Sherin, M. G., & Drake, C. (2009). Curriculum strategy framework: Investigating patterns in teachers’ use of a reform‐based elementary mathematics curriculum. Journal of Curriculum Studies, 41(4), 467-500.

 

Hello, everyone. Happy new year! I’m back at the blog after a much-needed winter break.

This week I’ve been thinking more about digital curriculum materials and adaptations (ideas I talked about in this post and this post). When I talk about this area of my research interests to new people, I usually frame it as a question of how a digital medium might be used to create curriculum materials that are more flexible, thereby helping teachers to make adaptations according to their needs and contexts.

A natural follow up to such a description is, what does it mean for curriculum materials to be flexible? Oddly enough, I don’t think I’ve ever been asked that, despite giving that description a lot. It is a question I asked myself a few days ago, though. What are the kinds of flexibility that would be useful to teachers?

To this point, I’ve always been pretty focused on the idea of teachers changing the order in which the content is presented. Maybe kids need to be able to measure to the nearest half-inch to do an art project next week, for example, and so a teacher wants to teach a lesson on that. If she moves the lesson a unit earlier in the sequence, what are the repercussions of that? In what other ways would the sequence need to be adjusted to make sure it still follows a coherent progression? I’ve always thought — and still think — that is must be possible to design a system that gives intelligent feedback to teachers about potential impacts of sequence changes. It’d be a way to reveal the curriculum designer’s intentions, as described by Hoyles and Noss (2003) (and much later and less thoroughly by me, in this post).

I’m not the only one interested in the idea of building and maintaining coherent sequences of content — other researchers have talked about ways to do that in both mathematics (Confrey, Gianopulos, McGowan, Shah, & Belcher, 2017) and science (Shwartz, Weizman, Fortus, Krajcik, & Reiser, 2008). I haven’t lost interest in that idea. In recent days, however, I’ve been thinking about other kinds of changes and adaptations teachers might want to make to curriculum materials, and realizing that my thinking about flexibility, to this point, has been pretty inflexible.

In a recent conversation with some curriculum development colleagues, we were discussing one of the most pervasive and ongoing tensions in curriculum development work. On one hand, we aim to always provide adequate features and information to support all teachers in implementing lessons. On the other hand, we want to communicate that the suggested discussion questions, samples of student work, and other information are intended to support teachers in thinking about the lesson — not to script it. More information is — in some ways — more support, and yet it can also seem like an attempt to take the agency away from teachers, which is something we don’t want.

This led me to wonder whether there were certain types of information that are potentially useful to some teachers, but perceived as scripts or mandates to others. Feiman-Nemser (2001) points out that teachers have different professional development needs across the course of their careers. Newer teachers, for example, may benefit from more information about how a lesson might play out than more experienced teachers. Could the number of sample discussion questions shown be something teachers would adapt to their needs? What about whether or not information about how to support to English-language learners is shown? This could be a whole different class of adaptations that has nothing to do with how content is sequenced.

I was also reminded a few weeks ago that there is research showing that teachers interact with curriculum materials in different ways at different points of the planning and implementation process (e.g., Sherin & Drake, 2009). I have been pretty focused to this point on adaptations that teachers might make while planning, but limiting my thinking to planning activity disregards the importance of in-the-moment decisions that make up so much of a teacher’s work. Listening to students’ thinking can lead a teacher to change a task or learning goal in the moment. Such a change is an adaptation to curriculum, but could it also necessitate an adaptation to the curriculum materials? If so, how could curriculum developers support such an adaptation?

All in all, I find myself thinking in a whole new way about the idea of how curriculum might be made more flexible. What other kinds of flexibility have I not thought about yet?

References

Confrey, J., Gianopulos, G., McGowan, W., Shah, M., & Belcher, M. (2017). Scaffolding learner-centered curricular coherence using learning maps and diagnostic assessments designed around mathematics learning trajectories. ZDM – Mathematics Education, 49(5), 717–734. https://doi.org/10.1007/s11858-017-0869-1

Feiman-Nemser, S. (2001). From preparation to practice: Designing a continuum to strengthen and sustain teaching. Teachers College Record, 103(6), 1013–1055. https://doi.org/10.1111/0161-4681.00141

Hoyles, C., & Noss, R. (2003). What can digital technologies take from and bring to research in mathematics education. In Second International Handbook of Mathematics Education (pp. 323–349). https://doi.org/10.1007/978-94-010-0273-8_11

Sherin, M. G., & Drake, C. (2009). Curriculum strategy framework: Investigating patterns in teachers’ use of a reform‐based elementary mathematics curriculum. Journal of Curriculum Studies, 41(4), 467-500.

Shwartz, Y., Weizman, A., Fortus, D., Krajcik, J., & Reiser, B. (2008). The IQWST experience: Using coherence as a design principle for a middle school science curriculum. The Elementary School Journal, 109(2), 199–219.

 

Hello, everybody.

Tomorrow is the last day of my first semester as a PhD student. I survived! And I’m really happy that I’ve managed to post a blog entry every week. I hope to keep doing so next semester and throughout my graduate school career.

To close out the semester, before taking a couple of weeks off for the holidays, I thought I’d share a list of some of the things I’ve learned this semester. Not the ed psych or the perspectives on math ed or the research methods, but things I’ve learned about myself and about being a thoughtful and productive scholar.

Here goes.

1. Reading academic articles is not only about making sure you understand what they say, but also understanding what you think about them. I’ve explored the difference between content and practices in relation to mathematics education for a long while, but the distinction has become clearer to me in graduate school. Graduate study not really about content at all. The content is just a useful mechanism for learning how to think. Learning to clearly articulate what you think about the work of others is a major component to becoming a better academic writer.

2. Sometimes the key to making connections among articles is reading them with a lens the author did not necessarily intend. Academic work does not build on itself in a linear way, but rather in a widely sprawling way. Synthesizing studies that were all approached in the same way often does not lead to anything interesting. Making a unique contribution to the field can happen through empirical work, but also through making connections between seemingly different pieces by viewing them each through the same lens.

3. Citation management software is an academic’s best friend. If you’re in grad school and not using it, start. It will change your life. I spent 12 years reading academic articles that I promptly forgot about because I didn’t catalog them. In just one semester, I’ve built up a library that I regularly draw upon rather than starting from scratch in each new pursuit. That’s all thanks to my citation software.

4. One of the best pieces of advice I got before beginning graduate school was that I needed to treat it like a job. That means getting up at a regular time and getting myself to campus during working hours. This habit has not stopped the work from bleeding into my evenings and weekends, of course. But overall it has made the lifestyle manageable.

5. There are a variety of dimensions along which researchers arrange themselves. Positivist or interpretivist? Behaviorist, cognitivist, or socio-culturist? Theorist or practitioner? Choosing an area of research focus is much more intimately connected to developing a personal and professional identity than I ever could have imagined. Because of that, I’m having commitment phobia. It is going to take me a while to convince myself I’ve found the area where I want to stake my claim.

 

Thanks for taking the journey with me this semester. Happy holidays, and see you in January.

I have always been a little bit of an anomaly in my career field. Although I’ve worked on various education projects and materials for over ten years now, but I’ve never been a classroom teacher. I was a math major as an undergraduate student, with little interest in education at the time. It was only through a random search for “mathematics” in a job search engine upon graduation that I ended up with a temporary contract position in educational publishing. After that, I went to graduate school to get a masters in learning sciences, then to the university for ten years of work in curriculum development, and finally, this year, I started a PhD in educational psychology and educational technology. I taught a couple of recitation sections of a math course as an undergraduate senior, and I’ve taught brief lessons in various classrooms on occasion, but other than that, I have no teaching experience.

People ask me sometimes why I didn’t choose to go through a teacher ed program and teach for a few years once my interest in education started to develop. There are a couple of related answers to that question. One is that it felt somehow insincere to enter teaching with the explicit intention of leaving it after a couple of years. Another is that I didn’t (and still don’t) think I’d be particularly good at it. I find it difficult to develop good rapport with kids, and I am not a quick thinker. When I’m in a conversation that doesn’t go the way I expect, I am almost never able to respond intelligently in the moment. It takes me a while to work through things. That’s not possible when 30 students are sitting in front of you, waiting for reasonable answers to their questions.

The constant need for in-the-moment decision-making, in my opinion, is among the most difficult aspects of teaching. The very thought of it is one of the major reasons I never pursued teaching. The willingness and ability to handle the constantly changing course of conversation in classrooms is the thing I admire and respect most about teachers. I have always been too scared of the idea to even try.

As a researcher interested in processes of learning, I’ve always been curious about the ways in which teachers learn to be agile and responsive in their teaching. I know that it’s something that develops over time with practice and experience, but are there ways of helping that development along? How does that play out in teacher education?

This week I read a couple of pieces that answer that question, at least in part. Crespo, Oslund, and Parks (2011) asked pre-service teachers to imagine and write out narrative scripts of how they thought their lesson plans would play out in their classrooms. What would students give as answers to particular problems? What would the teacher say in response? How would the conversation progress toward the mathematical goals of the lesson?

The researchers explored the idea of having preservice teachers write out enactments, rather than focus exclusively on lesson plans, because they felt that the former would allow a different window into teacher thinking. “Consider the difference between writing out a teacher action plan and acting out that plan (even if on paper). Although both of these serve to map the intellectual journey and destination of a math lesson, they do so from different perspectives. The first takes a bird’s eye view perspective, while the second takes a ground level viewpoint” (Crespo, Oslund, & Parks, 2011, p. 121).

I found this contrast fascinating, because it clearly articulated the difference between planning lessons and teaching lessons in a way that starts to get at the challenges of in-the-moment thinking that happens while teaching. Writing out scripts of possible enactments is an interesting way to prompt teachers to think about the possibilities of that in-the-moment work, in a context that doesn’t have the same time pressure for thinking through responses.

The Crespo et al. (2011) article discusses script-writing as a method for gaining a window into teacher thinking. That is, they discuss it as more of a research tool than a teacher education tool. When I brought up the prospect of using scripting as a technique for helping teachers develop skills in responding to students in the moment, my classmates and instructors rightfully brought up a concern that writing out a script might make teachers less apt to deviate from that script if something plays out differently than they expect in the classroom. I understand this, and so don’t really believe that hypothetical scripting of lesson should be part of daily lesson planning. I do, however, still wonder if making the creation of multiple possible scripts for the same discussion, done in the right context at the right time, could be beneficial to developing flexible thinking, that in turn helps teachers to be flexible in moment-to-moment thinking.

The second article I read this week that spoke to this particular issue was Lampert et al.’s (2013) study of rehearsal as a teacher education technique. Lampert et al. explain that rehearsal “can involve novices in publicly and deliberately practicing how to teach rigorous content to particular students using particular instructional activities” (p. 227). During rehearsals, preservice teachers teach a lesson to their peers and teacher-educators, with the teacher-educators calling out feedback and sometimes interrupting and pausing the lesson to discuss what just happened and ways a situation might have been handled differently. Rehearsal, like scripting, was appealing to me because it represents a way to examine and develop in-the-moment thinking with a built-in capacity to give teachers a bit of extra time to think things through and consider possibilities.

What do you think? Is one of the keys to developing skills in responsive, in-the-moment decision-making providing ways to slow down time a bit, as in scripting and rehearsal? What other ways of developing skills have you heard about or experienced?

And if you’re a teacher: Does it get easier over time? What has helped you feel prepared for the unknown trajectories of conversation in a classroom?

References

Crespo, S., Oslund, J. A., & Parks, A. N. (2011). Imagining mathematics teaching practice: Prospective teachers generate representations of a class discussion. ZDM – International Journal on Mathematics Education, 43(1), 119–131. https://doi.org/10.1007/s11858-010-0296-z

Lampert, M., Franke, M. L., Kazemi, E., Ghousseini, H., Turrou, A. C., Beasley, H., … Crowe, K. (2013). Keeping It Complex: Using Rehearsals to Support Novice Teacher Learning of Ambitious Teaching. Journal of Teacher Education, 64(3), 226–243. https://doi.org/10.1177/0022487112473837

 

About six months after completing my master’s degree, I went to a holiday party thrown by one of my former classmates. In my particular program, master’s students take many classes with first-year Ph.D. students. The attendees at the party were a mix of the Ph.D. students I knew — now in their second year of study — and new master’s students that I had not met before that night. At some point, one of the Ph.D. students, who was my officemate the year before, made a comment to one of the master’s students that I still remember.

“We have ten weeks to finish the work of a quarter, right? Katie was always done in seven.”

While finishing three weeks ahead was an exaggeration of my general pattern, I couldn’t deny that I was usually ahead of the pack in terms of finishing course requirements. It wasn’t that I was faster than everyone else when it came to reading or writing. I may be a bit above average on writing speed, but I would bet that I’m below average on reading speed, and usually slow to organize my thoughts, as well. Speed wasn’t the issue. And I really struggled with a lot of the coursework in grad school. Ease versus difficulty wasn’t the issue, either.

The reason that I tended to finish early, and still tend to do this, is this: I live in perpetual fear of running out of time.

While I do have isolated bouts of procrastination, it definitely isn’t my biggest vice. I start projects the day they are assigned just in case I end up making a false start and need more time than I anticipate. If I happen to have extra time during one week, I tend to read ahead in my courses just in case something big comes up the next week. I love to be done early. That’s the only time I feel like I can be justified in not working on something.

I have long known this about myself, but I started to think about it in a bit of a different way after revisiting the work of Carol Dweck (1999) and Jo Boaler (2012).

Dweck’s (1999) work focuses on the idea of fixed versus malleable conceptions of intelligence. Student who believe that intelligence is malleable and they can become more intelligent over time are more likely to choose and persist at challenging tasks. Student who believe that intelligence is a fixed tend to avoid challenging tasks. Among Dweck’s more prominent findings is the fact that the kind of praise given to students when they succeed can have a strong effect on their conceptions of their own ability and their reactions to failure. Students who are praised for being smart develop a fixed theory of intelligence, and tend to react to failure by starting to believe they are not smart after all. Students who are praised for their effort develop a malleable theory of intelligence, and tend to persist in the face of challenge and try again upon failure. Building on Dweck’s theory and findings, Boaler (2012) has conducted studies of interventions aimed at helping students develop a malleable view of intelligence, or a growth mindset.

Dweck and Boaler are among my academic heroes. A big part of my reason for starting a career in education research is my desire to help put an end to the prevalent I’m just not a math person narrative, and hopefully help to prevent a similar I’m just not a computer science person narrative from becoming as common. Growth mindset interventions have a lot of promise in this regard.

At the prompting of one of my instructors earlier this year, I took some time to think about whether I have a growth mindset. I was pleased to come to the conclusion that I think I do. There isn’t much that I don’t think I could learn, if I took the initiative to do so. What I found interesting about this reflection, though, was the caveat I felt I had to add:

I could learn just about anything…. as long as I had enough time. Some things might take me a very, very long time.

This was interesting to me from both personal and professional perspectives. On a personal level, it helped me to explain my perpetual anxiety about running out of time and how that coexists with a solid sense of my own academic ability. I think I’m perfectly able. I just think that there’s always a risk of things being slow and difficult. Not impossible, but slow and difficult. I’ve never articulated that belief before. It’s helped me to reconcile my belief in malleable intelligence with the existence of sports stars, musical prodigies, and the like. Everyone can learn anything they like, with sufficient time, resources, and motivation — but this does not mean that each person will have to do the same amount of work to get there. There is such a thing as a natural proclivity. The power of growth mindset is that it shifts this idea of natural proclivity from separating the world into cans and cannots — something that is false — to identifying the those who have a quicker path to being highly skilled among a huge population of capable people.

From a professional perspective, this realization helped me to think more carefully about the problems that growth mindset work does and does not help to solve. I think many students carry around a belief that they are not good — and cannot be good — at mathematics, and that particular issue can be addressed with growth mindset work. Even so, the interventions won’t remove all potential anxieties about mathematics. Even if a student comes to believe he or she can indeed learn mathematics, that won’t necessarily lead to the belief that it will be easy, enjoyable, or worthwhile.

On one hand, perhaps this is ok. The goal has never been for all students to become mathematicians — just to help them attain a certain level of mathematical fluency and efficacy. One can hope that any overpowering anxieties about slowness and difficulty could be kept at bay through K-12 education. At that point, perhaps a greater number of students will pursue mathematics-related careers, and the rest will have reached a point of mathematical literacy that makes them effectively able to interpret and use mathematics to understand day-to-day issues.

On the other hand, there’s something about this line of thinking that bothers me. Is it a slippery slope? Is “Everyone can do math, but some people can do it more easily and faster than others” really a better narrative than “Some people just aren’t good at math”? I’m not so sure. My perpetual assumption that I need to plan for things to be difficult and time consuming isn’t something I want all kids to be carrying around.

The simplistic solution is to just change the narrative to “Everyone can do math,” and leave it at that. The decision of whether or not to pursue mathematics is then up to the student, and hopefully any decisions made won’t be based on worries about fixed intelligence.  I just worry that the second part, “but some are better than others,” will be carried around after it, implicitly, if we don’t address it head on. Then we won’t really have fixed the problem — just shifted the barrier a bit.

I am sure you can tell by my rough writing here that I have not worked out all of my thoughts on this. But it’s something I’ve been thinking about, particularly when considering how I can use lessons learned from mathematics education to help to prevent a not a CS person narrative from taking hold as CS is introduced into K-12 schools.

References

Boaler, J. (2013). Ability and mathematics: the mindset revolution that is reshaping education. FORUM, 55(3), 143-152.

Dweck, C. S. (1999). Caution—Praise Can Be Dangerous. American Educator, 23(1), 4–9.

Yesterday I had a conversation with some fellow curriculum developers about the potential impact of translating hands-on activities into a digital environment. It was quite interesting and engaging — and like most interesting conversations I have these days, it left me much more confused than I had been when the conversation started.

We started by talking about 3-dimensional geometry, and the potential perils of studying it 2-dimensional representations on paper or on a screen. Though none of us had research at our fingertips that spoke to this (although I’m reasonably certain such research exists), at first we generally agreed that there are likely important benefits related to manipulating physical, 3-dimensional objects when studying 3D geometry and volume.

Then someone mentioned the idea of a digital environment with a 3D rendering of a physical object. What about a cube, for example, that can be rotated and viewed from any angle? Does this have the same benefits as handling a physical cube?

In other words, is 3D versus 2D the difference that matters? Or is it dynamic (and thus manipulable) versus static? Or is the really important difference the one that started this conversation in the first place: physical versus digital?

If the critical factor is 3D versus 2D, and true 3D representations are what work best for learning, then certainly the prospect of designing a curriculum that is delivered entirely digitally is a problem. This sort of argument is often used against the trend toward digital curriculum products in classrooms, especially for young kids. But this conversation with my colleagues helped me articulate something that has always bothered me about that argument. It’s this: if 3D versus 2D is the critical difference, than digital curricula aren’t the only curricula with problems. Traditional print curricula so often rely on 2D representations of 3D objects — static ones, on paper. So if there are going to be 2D representations anyway, aren’t the digital, dynamic, 2D representations just as good as the paper, static, 2D representations — and perhaps even better?

This chain of reasoning led me into thinking about digital alternatives to other physical objects used in classrooms. If the object of study isn’t something 3-dimensional, do the same kinds of concerns apply? Take base-10 blocks, for example. The physical blocks are 3-dimensional and the digital blocks are 2-dimensional, but that difference doesn’t seem to matter in this case, since neither version is a representation of a 3D object, but rather of an abstract number. Both versions are manipulable, but the particular manipulations are different. With the physical blocks, if children want to think of 1 ten as 10 ones or vice-versa, they must exchange a long (or ten block) for a cube (or one block). In many of digital versions of the blocks, if children want to think of 1 ten as 10 ones or vice-versa, they are able to break apart 1 long or put together 10 cubes. In that sense, the digital blocks are more dynamic than the physical blocks.

Sarama and Clements (2009) further point out that the action of breaking a long is closer to the mental actions children must make on numbers to add and subtract than the action of exchanging a long is. Since the first step toward abstract understanding of a concept is typically interiorization, or the ability to carry out a process through manipulations of mental representations (Sfard, 1991), this “closeness” to the mental manipulations of numbers could be important.

A study by Bouck et al. (2017) gives another example of how a digital tool accelerated the process of interiorization, in this case for students with mild intellectual disabilities. Previous research had shown that leading these students through a concrete → representational → abstract sequence was effective in supporting learning of addition of fractions with unlike denominators. The concrete phase involved physical manipulatives, the representational phase involved creating drawings, and the abstract phase involved symbol manipulation. This study found, however, that when digital manipulatives were used, the representational phase could be skipped entirely. For three out of four students in the study, a virtual → abstract sequence was effective. This suggests that the digital manipulative helped students to interiorize the process of fraction addition.

My point in giving these examples, I suppose, is to illustrate why I’ve come to think that the debates about digital versus physical mathematics manipulatives are placing too much emphasis on physical versus digital as the difference that matters. In some cases, digital versions have affordances that physical versions do not. I’m sure it’s also that case in reverse.

I’ve been struck, in the past, as I’ve noted that there really aren’t many studies that pit physical and digital versions of manipulatives against each each other in terms of effectiveness. It seemed like such an easy and straightforward area of inquiry. Now I think I’m coming to understand why so little research is formulated that way. Studies that show a difference between physical and digital tools for learning would only open more questions about which affordances of each version led to the differences. Digital versus physical isn’t really what matters.

References

Bouck, E. C., Park, J., Sprick, J., Shurr, J., Bassette, L., & Whorley, A. (2017). Using the virtual-abstract instructional sequence to teach addition of fractions. Research in Developmental Disabilities, 70(June), 163–174. https://doi.org/10.1016/j.ridd.2017.09.002

Sarama, J., & Clements, D. H. (2009). “Concrete” computer manipulatives in mathematics education. Child Development Perspectives, 3(3), 145–150. https://doi.org/10.1111/j.1750-8606.2009.00095.x

Sfard, A. (1991). On the Dual Nature of Mathematical Conceptions: Reflections on Processes and Objects as Different Sides of the Same Coin. Educational Studies in Mathematics, 22, 1–36. https://doi.org/10.1007/BF00302715

 

Recently I’ve been thinking about the implications of feeling visible or invisible, and how the implications vary by context. On one hand, invisibility can be a sign that a community finds a person or population uninteresting, inconsequential, or even necessary to hide. (Think Mr. Cellophane.) On the other hand, invisibility can be a form of protection. (Think of invisibility as a superpower.)

I started thinking about this after reading two papers on the role of race in mathematics education. First came Maisie Ghoulson’s (2016) striking piece on intersectionality, where she demonstrates the ways in which Black girls and women are invisible in mathematics. The invisibility isn’t inevitable. Rather, it is constructed. Ghoulson points out that Black women are used as props to justify research that excludes them. When researchers discuss the difficulties facing the Black community as a whole and then pivot to discussing the particular issues facing Black men, for example, Black women drop out of the discussion. Because of this, we don’t know how Black women are doing in mathematics. We presume they’re doing fine, when really, we have simply made them invisible.

This piece, naturally, got me thinking that invisibility is perilous.

A few days later, though, I read a study by Niral Shah (2017) about the ways that racial narratives relate to mathematics education. There’s a prevalent narrative, for example, that Asian students are particularly good in mathematics, and another that says Black students are not. Shah’s study found that these narratives about the role of race in mathematics education are quite often evoked in relation to each other in ways that imply a hierarchy. One of the excerpts from his study, for example, was this, from a Black student: “Like I’m Black but I’m good at math. So are you not going to ask me for help because I’m not Asian?” (Shah, 2017, p. 23). This statement places Asian students high on the hierarchy and Black students low, giving each group not just an absolute position, but a position relative to each other. Meanwhile, narratives about White students did come up occasionally, but not nearly as often. The White students, in this case, were invisible — which, in a sense, gave them a pass from being ranked according to their race.

So, perhaps invisibility is not always perilous? What makes the consequences so different for Black girls than for White students? I know, of course, that the contexts of the invisibility are quite different. Invisibility from attention in research is different from invisibility in racial narratives. That alone, I suppose, could be enough to make this comparison uninteresting. But something about this explanation just wasn’t satisfying to me. It was as if the comparison was nagging at some dusty memory in the back of my mind that I couldn’t quite identify.

I was lucky enough to have the chance to speak to Dr. Shah about his article a few days ago. I posed this comparison to him and asked what he thought. He said lots of interesting things in his response, but the thing that really gave me a light bulb moment was this: Dr. Shah suggested that perhaps thinking of White students as invisible isn’t the most illuminating way of thinking about visibility in his study. Rather, maybe the effects of the racial narratives are to make Asian students hyper-visible. Further, Dr. Shah said he wasn’t convinced that being hyper-visible was beneficial to anyone.

This made perfect sense to me, and helped me think differently about the narratives about Asian students and those about Black students. For the Asian students, the narratives could lead to high expectations based on race that, for some, could be hard to attain and lead to undue pressure. For Black students, the narratives could lead teachers to devalue their contributions to mathematics discussions, which in turn could lead to a kind of invisibility.

Thinking about this also surfaced that nagging memory I suspected was in my head somewhere. When Dr. Shah used the term hyper-visible, I suddenly remembered writing this Facebook post on the day that Hillary Clinton got the Democratic party nomination for President:

I know what it means to be hyper-visible, and while the consequences are different than being invisible, they can still have detrimental effects.

Once again, I find myself with a new frame for thinking about a complex issue related to teaching and learning. Grad school is good for that.

What do you think? What are the potential effects of invisibility and hyper-visibility? What does this mean for teaching and learning in classrooms?

References

Gholson, M. L. (2016). Clean Corners and Algebra: A Critical Examination of the Constructed Invisibility of Black Girls and Women in Mathematics. The Journal of Negro Education, 85(3), 290–301.

Shah, N. (2017). Race, Ideology, and Academic Ability: A Relational Analysis of Racial Narratives in Mathematics. Teachers College Record, 119(7), 1–42.

The past two weeks, I have had a hard time concentrating on any one task. It’s the point during the semester when several papers and projects are coming due at once. I’ve started drafts of many of them. Try as I may to concentrate on one at a time, my subconscious never seems to be working on the same one as my conscious brain. In the middle of a sentence about computational thinking, I suddenly realize one more thing I should have said about digital curriculum resources. Oh, and that thing I just read about qualitative research methods? I really need to write down the way in which it’s connected to that study of abstraction I read last week.

I was reflecting on this phenomenon tonight, and thought of a blog post I wrote many years ago — on November 22, 2010, to be exact. The following text comes from the post, where I’m trying to decide why so many university professors wear similar clothes day after day:

“Over the past few years, I have had the privilege of working with some of the most brilliant minds in my field. My bosses are the rock stars of mathematics education. And I can tell you the one thing they have in common, the one thing that has set them apart: they are always thinking. Always. Their minds work like conveyor belts; when they solve one problem, all the rest are waiting on the belt. They never stop thinking about their work.

This means that the rest of the things that us average joes think about — like the clothes that we wear — don’t get any time in the conscious brain. Academians just operate on autopilot. You know how, when you wake up late and have to rush out, you end up having no memory of choosing your clothes? I imagine that it’s like that for academians all the time.

People in all walks and phases of my life have branded me as a smart person. I was on top of my class in high school, and no one was surprised when I graduated from college cum laude or got accepted to a prestigious graduate school. Many of these people are probably expecting me to get a doctorate someday. It’s just what smart people do. But this line of thought has only made me more sure that academia is not where I belong.

The people that succeed in academia are the ones that choose their clothes on autopilot. I, on the other hand, go to autopilot while I am running so that I can spend that time deciding what I will wear that day.

I could never become a research scientist or professor. I love cognitive science and I love math — but I also love the moments when I can stop thinking about them.”

 

Are you laughing? I laughed. I wonder when I crossed the line. I never stop thinking about math and cognition and learning now. But hopefully that means that I have ended up where I belong.

As you have probably noticed by now, the role of context and applications in mathematics education is a key interest of mine. Over the years I have come to believe more and more firmly that not all mathematical learning has to be in context, and that it is counterproductive to attempt to teach everything in context. Forcing context on mathematics often leads to meaningless and contrived problems that almost certainly do nothing to enrich learning.

On the other hand, I also believe that when clear and relevant connections can be made between mathematics and other content domains or broader everyday-life issues, they should be. Mathematics, after all, was developed to solve real problems, and some connections can be productive. It is helpful, for example, for children to think about putting things together when they do addition and creating equal groups when they divide.

This seems like a very pragmatic, and maybe even obvious, position to take: Use context when it makes sense. Yet many times in the course of my career I’ve been struck by how difficult it is to strike the right balance. Take, for example, the relatively simple mathematical topic of graphing a linear inequality. (Full disclosure: What follows is a retelling of the process I went through to write a lesson on this topic during my curriculum development years.*)

To graph something like x > 3, you draw a number line, draw a circle on the 3 mark, and shade everything that’s greater than 3, like so:

And it’s pretty simple to come up with a context for an inequality. For example, suppose a library has a rule that a patron can check out no more than 4 books at a time. If b is the number of books, we can represent the situation with the inequality b ≤ 4. A graph of that inequality looks like this:

But wait… if this is a representation of the context, then we really shouldn’t have any values of b less than 0. You can’t check out -2 books. So maybe this:

Well, and you can’t really check out a fractional part of a book, so what we really want is this:

Okay. Now we’ve got a reasonable representation. But creating one brought out some other mathematical ideas, like defining domains and discreteness versus continuity, that I didn’t expect when I set out.

I don’t mean to argue that it was too hard to make a context work in this instance. My colleagues and I were able to finesse these ideas into a lesson that we thought did justice to both what we intended to be the main mathematical idea (graphing inequalities) and these other mathematical ideas. Rather, my point is that the connection between the mathematics and the context wasn’t simple. There wasn’t a one-to-one correspondence.

My point in telling this story is this: Lately I’ve been thinking that perhaps a lot of my troubles — and to the extent that I can generalize, the troubles of the mathematics education community — in connecting mathematics and context is that we’re focused on finding a perfect match. We dismiss potential ways of connecting mathematics to life outside of school because we’re afraid that either the mathematics or the context becomes skewed, oversimplified, or contrived. But maybe it doesn’t need to be. Maybe instead of adjusting the math or the context to achieve a fit, we can acknowledge that the match is imperfect, and take it for what it is.

I started thinking about this last week after reading a book chapter describing a researcher’s experience teaching a class on mathematics for social justice to high school seniors in a Chicago community. Gutstein (2012) describes how he structured the course around “generative themes” that were suggested by the students in the class. I was particularly intrigued by his discussion of a unit on the spread of HIV/AIDS, where students used complex mathematical models to simulate the spreading of the disease and had in-depth discussions about some of the more striking statistics showing the disproportionate effects of the disease on certain populations.

At the time, he was concerned that the mathematics and the context were not well aligned: “[S]tudents did not need to model HIV/AIDS to understand the disease, grasp the disproportionate impact on certain populations, or not blame Black women” (Gutstein, 20102, p. 35). Later, he considered the idea that this may not be a problem, but rather just an example of a different kind of connection: “At times, we use mathematics to explain social things (like the election being stolen), at other times, we use social analysis to explain mathematics (like high AIDS rates). The point here is, I think, that you cannot easily explain one without the other” (p.35).

Sometimes, mathematics directly helps solve a social problem (like explaining the results of the 2008 election). Other times, a context helps establish why mathematics might be useful (like AIDS statistics motivating a study of mathematical models). In either case, though, the match isn’t perfect. Still, the lack of a perfect match does not diminish the connection’s utility.

As for most of the musings I write about in this blog, I am not sure where this realization leaves me or how I would do anything in my curriculum development work differently if I could go back and do it again. I don’t have any easy strategies for opening up my own thinking about connections to context. Instead, I’ll just end with one more example that struck me as I read today.

In an article about ways in which the mathematics education research community can be more attentive to issues of intersectionality — that is, the particular issues and challenges faced by those in two or more overlapping marginalized groups, such as Black women — Bullock (2017) says the following: “The idea of multiple burden speaks to intersectionality’s key concern that racism, sexism, and other forms of oppression, when considered in parallel, appear additive, but those who experience these oppressions in combination endure multiplicative effects” (Bullock, 2017, p. 31).

This article has nothing whatsoever to do with any of the issues I discussed in this post. She wasn’t aiming to make a connection between mathematics and social justice issues (at least not in the same way Gutstein (2012) was). Still, her framing of the issue in terms of a mathematical idea — specifically, the difference between additive and multiplicative growth (5 + 5 versus 5 * 5, for example) — really brought her point home for me. I understand intersectionality better than I did before.

The connection between intersectionality and multiplicative growth isn’t perfect. But it is powerful.

References

Bullock, E. C. (2017). Beyond “ism” Groups and Figure Hiding: Intersectional Analysis and Critical Mathematics Education. In A. Chronacki (Ed.), Proceedings of the 9th International Mathematics Education and Society Conference (MES9, Vol 1) (pp. 29–44). Volos, Greece: MES9.

Gutstein, E. R. (2012). Mathematics as a Weapon in the Struggle. In O. Skovsmose & B. Greer (Eds.), Opening the Cage: Critique and Politics of Mathematics Education (pp. 23–48). Rotterdam, Netherlands: Sense Publishers.

 

*Shout out to my colleagues Andy Isaacs (my most loyal reader and commenter!) and Sarah Burns, who were involved in this discussion.

When the Common Core State Standards for Mathematics (CCSS-M) were first released, one of the aspects of the reactions that I found most interesting was the diversity of reasons for opposing them. Education researchers and developers, like myself, were dismayed at the nearly exclusive focus on arithmetic in elementary school, or the undue burden placed on the middle school grade band when content was both moved up from elementary school and down from high school, or likely some other issues related to content distribution. Teachers shared some of these content concerns and also worried the standards would only place greater emphasis on standardized tests. Conservative politicians disliked the standards because they were a strong step in the direction of federal control of education. Most of the criticism I heard from the general public, though, related to the idea that the standards made mathematics unduly complicated or even incomprehensible.

This video is one example of the kinds of critiques that floated around the Internet. It’s not very long, so if you can, take a minute or two to watch it. In a nutshell, it compares the steps for the subtraction algorithm most adults learned in school to the steps of a different approach, when applied to a particular problem. The new approach — a method that I and many of my math education colleagues call counting up — comes off looking complicated and nonsensical in comparison to the traditional method.

A friend of mine posted a link to the video on my Facebook wall and asked my opinion. Here was my response. (Spolier alert: I found videos like this super annoying at the time.)

I was annoyed, first of all, that the video made it sound like this method was the new standard, which isn’t true. The standards still require students to add and subtract with the same traditional algorithm as always by the end of fourth grade. It’s just that before that, there are standards that specify that students should add and subtract (and later, multiply and divide) using more generalized strategies that help illuminate conceptual understanding of the operations. For example, consider this first-grade standard:

Add within 100, including adding a two-digit number and a one-digit number, and adding a two-digit number and a multiple of 10, using concrete models or drawings and strategies based on place value, properties of operations, and/or the relationship between addition and subtraction; relate the strategy to a written method and explain the reasoning used. Understand that in adding two-digit numbers, one adds tens and tens, ones and ones; and sometimes it is necessary to compose a ten. (CCSSI, 2010, p. 16)

That’s as specific as the standards get when it comes to prescribing computation strategies (until they require the standard, familiar algorithms later). So the video is based on a false premise. That’s the first problem.

Later, a comment from a friend on the same Facebook thread led me to respond to the second, and probably more important problem I noted at the time: the fact that the method presented in the video is based on kinds of everyday reasoning that make perfect sense in some situations.

So, the second thing that really bothered me was the way that the counting-up method was (likely deliberately) set up to look confusing, when the same kind of argument could easily be made in the other direction. I felt that videos like this were masking the value of alternative strategies when I have, in my own personal and professional experiences, seen such strategies really help students see mathematics as something other than a set of procedures to be memorized and applied.

Those were my arguments pushing back on criticism of alternative computation methods at the time. I still agree with them, but also admit that they don’t always change people’s minds. My kid doesn’t like this stuff, they tell me. You’re saying it’s better and equally clear, but it’s not working for my kid, and what’s worse is that I can’t help with homework. It makes both of us feel helpless.

I’m sympathetic to these concerns, and haven’t had a better response in the past than, Hang in there. I knew it was true that these alternative methods and ideas were not magically going to make every kid suddenly understand computation in a new way. Education is not so simple. I was claiming that methods like counting-up subtraction often made sense — but what about the cases when it doesn’t?

I read a few things in the past few months that got me thinking about this. First, I read the first three chapters of Jerome Bruner’s Acts of Meaning. In his third chapter, as he constructs an explanation for patterns of language acquisition in young children, Bruner (1990) points out that from infancy, children have a strong tendency to devote more attention to things that are novel:

[W]hen [children] begin acquiring language they are much more likely to devote their linguistic efforts to what is unusual in their world. They not only perk up in the presence of, but also gesture toward, vocalize, and finally talk about what is unusual. As Roman Jakobson told us many years ago, the very act of speaking is an act of marking the unusual from the usual. (p. 78-79)

Bruner’s text is dense and sometimes difficult to interpret, but this passage made perfect sense to me. We do attend to what is novel. It’s one of the ways we sort through the enormous amount of information we perceive and decide what needs attention.

I didn’t connect this to the Common Core criticisms, though, until just a day or two ago. I read a study about treating bilingualism as a resource in mathematics classrooms that mentioned the very passage from Bruner that I quoted above. In response to the Bruner quote, Dominguez (2011) says, “This may explain why in most mathematics classrooms, students barely talk—they rarely do things with words—as they may be dealing primarily with the usual, that is, repeated exercises of the same kind” (p. 310). This response, like Bruner’s original point, made a lot of sense to me. Familiarity is not always a good thing. It doesn’t always lead to good experiences.

Perhaps this is another way of thinking about the potential benefits of conceptually-based computation methods like counting up. I’ve been focused on explaining why it is not as confusing as some might think. But the other side of that coin is that for some students and in some circumstances, it will be new and confusing. But in the right dosage, that’s ok — even a good thing.

New is what gets people talking. Talking is what gets people learning.

I know it will probably seem like a hollow response to the parents wanting to help kids with their mathematics homework and feeling incapable of doing so. But it at least feels a bit more well-rounded than my previous response insisting that these conceptual methods are not so confusing.

References

Bruner, J. (1990). Entry into Meaning. In Acts of Meaning (pp. 67–97). Cambridge, MA: Harvard University Press.

Common Core State Standards Initiative (CCSSI). (2010). Common Core State Standards for Mathematics. Retrieved from http://www.corestandards.org/Math/ on 1 March 2017.

Domínguez, H. (2011). Using what matters to students in bilingual mathematics problems. Educational Studies in Mathematics, 76(3), 305–328.